Content not available in English
En cumplimiento de lo dispuesto en el artículo 73 del Reglamento de Ejecución (UE) n.º 404/2011 de la Comisión, de 8 de abril de 2011, que establece las normas de desarrollo del Reglamento (CE) n.º 1224/2009 del Consejo por el que se establece un régimen comunitario de control para garantizar el cumplimiento de las normas de la política pesquera común, se establece la necesidad de averiguar el peso medio de los palets/jaulas utilizados para pesar el desembarque de los productos pesqueros congelados. Es este sentido, y para realizar una estimación del peso medio de las jaulas y de los palets, hay que realizar un plan de muestreo basado en la selección aleatoria de palets/jaulas y su pesaje en vacío.
Igualmente, para determinar el total descargado por un buque que faena en aguas de NAFO, se realiza el pesaje de las cajas llenas de pescado y se descuenta el peso de la caja en vacío (incluyendo plásticos y flejes), calculado este último según el correspondiente plan de muestreo para embalajes. El destare del pesaje trae a veces diferencias de criterio entre los inspectores de pesca marítima y los armadores de los buques. Es por ello que se plantea realizar un muestreo de cajas en vacío que permita determinar su peso medio, para todos los buques y en todas las descargas.
Esta Dirección General ha resuelto publicar en el «Boletín Oficial del Estado», el plan de muestreo de taras de jaulas/palets, que figura como anexo I y el procedimiento para la determinación del peso medio de las cajas de pescado que figura en el anexo II a la presente resolución del procedimiento para las descargas de pescado congelado proveniente de las áreas NAFO y NEAFC.
Esta resolución causará efecto a partir del día siguiente al de su publicación en el «Boletín Oficial del Estado».
Madrid, 23 de octubre de 2019.–El Director General de Ordenación Pesquera y Acuicultura, Juan Ignacio Gandarias Serrano.
1. Introducción.
El artículo 73 del Reglamento 404/2011 por el que se establece las normas de desarrollo del Reglamento (CE) 1224/2009 del Consejo, por el que se establece un régimen comunitario de control para garantizar el cumplimiento de las normas de la política pesquera común, menciona la necesidad de averiguar el peso medio de los palets/jaulas utilizados para pesar el desembarque de los productos pesqueros congelados. Es este sentido, y para realizar una estimación del peso medio de las jaulas y de los palets, hay que realizar un plan de muestreo basado en la selección aleatoria de palets/jaulas y su pesaje en vacío.
2. Objetivos.
El objetivo principal es la estimación de la media poblacional de los pesos de los palets/jaulas vacíos de una forma precisa sin tener que pesarlos todos.
3. Metodología.
Se va a distribuir la muestra a partir de la obtención de la estimación de la media poblacional usando un muestreo aleatorio simple:
Población: La población está compuesta por palets/jaulas vacíos que sirven para contener cajas de productos congelados Se supone que los palets/jaulas tienen pequeñas variaciones de peso debido al desgaste, a la absorción de humedad (si son de madera) o a cualquier otra causa externa. La población se considera el número de palets/jaulas utilizados en un desembarco.
Característica a estudiar: La característica que se va a estudiar de cada caja muestreada va a ser el peso neto de la caja. Con todos lo pesos muestreados se obtendrá una media muestral que es un estimador insesgado de la media poblacional. En otras palabras el valor esperado de la media muestral () es igual a la media poblacional
.
La media muestral se multiplica por el número de cajas de la población (cajas en el buque para una misma especie =) y se obtiene la estimación del total del peso poblacional:
Estimación del tamaño de la muestra: Se va a suponer que la distribución de los pesos sigue una Normal de media y desviación típica
. Esto indica que si obtenemos una media muestral
, la media poblacional
se encontrará en siguiente intervalo:
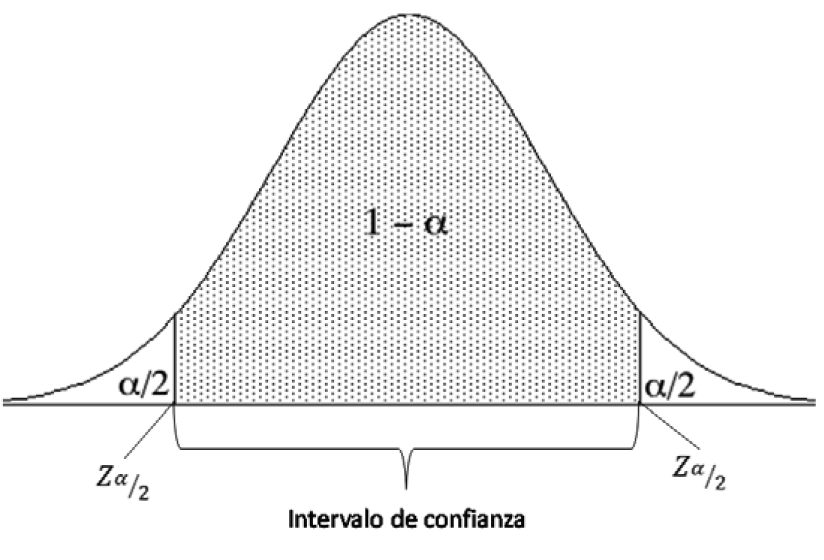
Podemos llamar a error máximo de muestreo (e).
Si se conoce la varianza poblacional , se establece el intervalo de confianza y el error máximo de muestreo se puede hallar el tamaño muestral:
Este tamaño se obtiene para tamaños de poblacion desconocidos o tan grandes que se supone que la poblacion es infinita, para tamaños de población conocidos hay que aplicar el factor de finitud:
El número de palets/jaulas a muestrear según el número de palets/jaulas que se desembarca es el siguiente:
Plan de muestreo para tara de palets/jaulas
| Palets/jaulas | Muestreo |
|---|---|
| 0-19 | todas |
| 19-27 | 10 |
| 28-50 | 12 |
| 51-75 | 13 |
| 76-100 | 13 |
| 101-110 | 14 |
| Por cada 100 adicionales | 1 |
Determinación del peso medio de las cajas de pescado en descargas NAFO
1. Introducción.
Para determinar el total descargado por un buque que faena en aguas de NAFO, se realiza el pesaje de las cajas llenas de pescado y se descuenta el peso de la caja en vacío (incluyendo plásticos y flejes), calculado este último según el correspondiente plan de muestreo para embalajes. El destare del pesaje trae a veces diferencias de criterio entre los inspectores y los armadores. Es por ello que se plantea realizar un muestreo de cajas en vacío que permita determinar su peso medio, para todos los buques y en todas las descargas.
Para hallar la media poblacional de las cajas se va a utilizar un muestreo aleatorio simple. En primer lugar se va a determinar el tamaño de la muestra dependiendo del tamaño de la población, del nivel de confianza y del error máximo que se quiera cometer.
2. Características de las cajas.
Se han detectado los siguientes tipos de cajas:
| TIPO DE CAJA | PESADA MEDIA |
|---|---|
| CAJA GRANDE NORMAL. | 1000 grs. |
| C. G. PARAFINADA TAPA Y FONDO. | 1250 grs. |
| CAJA MEDIANA NORMAL. | 500/750 grs. |
| CAJA ARMARIO TIPO EIRADO. | 400 grs. |
| CAJA TIPO H. GANDÓN ARMARIO. | 500 grs. |
| CAJA 3 PASTILLAS. | 1410 grs. |
| CAJA 2 PASTILLAS. | 550 grs. |
3. Determinación del tamaño muestral.
Antes de calcular el tamaño de la muestra necesitamos determinar varias cosas:
Tamaño de la población. Una población es una colección bien definida de objetos o individuos que tienen características similares. Hablamos de dos tipos: población objetivo, que suele tiene diversas características y también es conocida como la población teórica. La población accesible es la población sobre la que los investigadores aplicaran sus conclusiones.
Margen de error (intervalo de confianza). El margen de error es un estadístico que expresa la cantidad de error de muestreo aleatorio en los resultados de una encuesta, es decir, es la medida estadística del número de veces de cada 100 que se espera que los resultados se encuentren dentro de un rango específico.
Nivel de confianza. Son intervalos aleatorios que se usan para acotar un valor con una determinada probabilidad alta. Por ejemplo, un intervalo de confianza de 95% significa que los resultados de una acción probablemente cubrirán las expectativas el 95% de las veces.
La desviación estándar. Es un índice numérico de la dispersión de un conjunto de datos (o población). Mientras mayor es la desviación estándar, mayor es la dispersión de la población.
Podemos fijar de antemano todos los parámetros. La fórmula a utilizar es la siguiente:
Donde:
n es el tamaño de la muestra
Z es el nivel de confianza
N es el tamaño de la población
σ es la varianza
e es la precisión o el error máximo
Vamos a considerar que la población es suficientemente grande como para que el tamaño de la población no determine el de la muestra, consideramos una población infinita.
Obtenemos los siguientes resultados:
| TIPO DE CAJA | PESADA MEDIA (grs) | Σ | z (95%) | e | n |
|---|---|---|---|---|---|
| CAJA GRANDE NORMAL. | 1000 | 100 | 1,96 | 50,00 | 15,00 |
| C. G. PARAFINADA tapa y fondo. | 1250 | 125 | 1,96 | 62,50 | 15,00 |
| CAJA MEDIANA NORMAL. | 750 | 250 | 1,96 | 100,00 | 24,00 |
| CAJA ARMARIO TIPO EIRADO. | 400 | 40 | 1,96 | 20,00 | 15,00 |
| CAJA TIPO H. GANDÓN armario. | 500 | 50 | 1,96 | 25,00 | 15,00 |
| CAJA 3 PASTILLAS. | 1410 | 141 | 1,96 | 70,50 | 15,00 |
| CAJA 2 PASTILLAS. | 550 | 55 | 1,96 | 27,50 | 15,00 |
Como se puede observar para todos los casos el tamaño muestral es 15 excepto para las cajas de mayor variabilidad (caja mediana normal) que se tienen que pesar 24 cajas.
4. Selección de las cajas.
La selección de las cajas deberá realizarse de la forma más aleatoria posible evitando coger cajas consecutivas. En todo caso dependerá de la organización de los almacenes y de la posibilidad de identificar las cajas con un determinado número para realizar un «sorteo» aleatorio de las cajas.
State Agency Official State Gazette
Avda. de Manoteras, 54 - 28050 Madrid